Système en rotation
Présentation :
Le système étudié est composé de deux cylindres
coaxiaux de rayons R1 = 30 cm (fixe) et R2 (variable entre
10 et 27 cm). Sur le tambour de rayon R1 (vert) est enroulé
un fil inextensible de masse négligeable qui supporte une masse M1
= 0,5 kg. Sur le tambour de rayon R2 (jaune) est enroulé un
fil qui supporte une masse M2 (variable entre 200 g et 1 kg).
Pour étudier le mouvement, on peut analyser la tension des fils (voir la
machine d'Atwood).
On peut
aussi utiliser le théorème du moment cinétique.
On considère un trièdre direct Oxyz (Ox horizontal, Oy verticl
dirigé vers le haut et Oz normal au plan de figure). On pose q l'angle
de rotation du tambour, w sa vitesse angulaire, J
le moment d'inertie du tambour. Pour un tambour plein et homogène, J
est fonction des puissances quatrièmes de R1 et de R2.
Moment cinétique du système (par rapport à Oz) :
s = (J + M1.R12
+ M2.R22).w
Moment des forces appliquées : ( M2.R2 -
M1.R1).g
Donc : 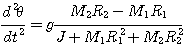
Le mouvement est uniformément accéléré. La rotation
a lieu dans le sens positif si le numérateur est positif (influence de
M2 prépondérante)
L'applet :
La valeur du moment d'inertie du tambour est calculée et affichée
par le programme.
Les zones de texte permettent de modifier les valeurs de M2 et de
R2. Le bouton [Départ]
lance l'animation avec les valeurs affichées dans les zones de texte.
Le bouton [Solution] permet
d'afficher la valeur de l'accélération angulaire du tambour et
la valeur de l'accélération de la masse M1. Vous pouvez
aussi vérifier le résultat de vos calculs.
Un chronomètre affiche la durée écoulée depuis le
moment ou les masses sont laissées libres (pas de vitesse initiale).
Cherchez des conditions d'équilibre du système.
Une pression sur le bouton de la souris
gèle l'animation, son relâchement permet de poursuivre.
 Retour au menu "mécanique".
Retour au menu "mécanique".